
Game Programming Techniques;
Introduction
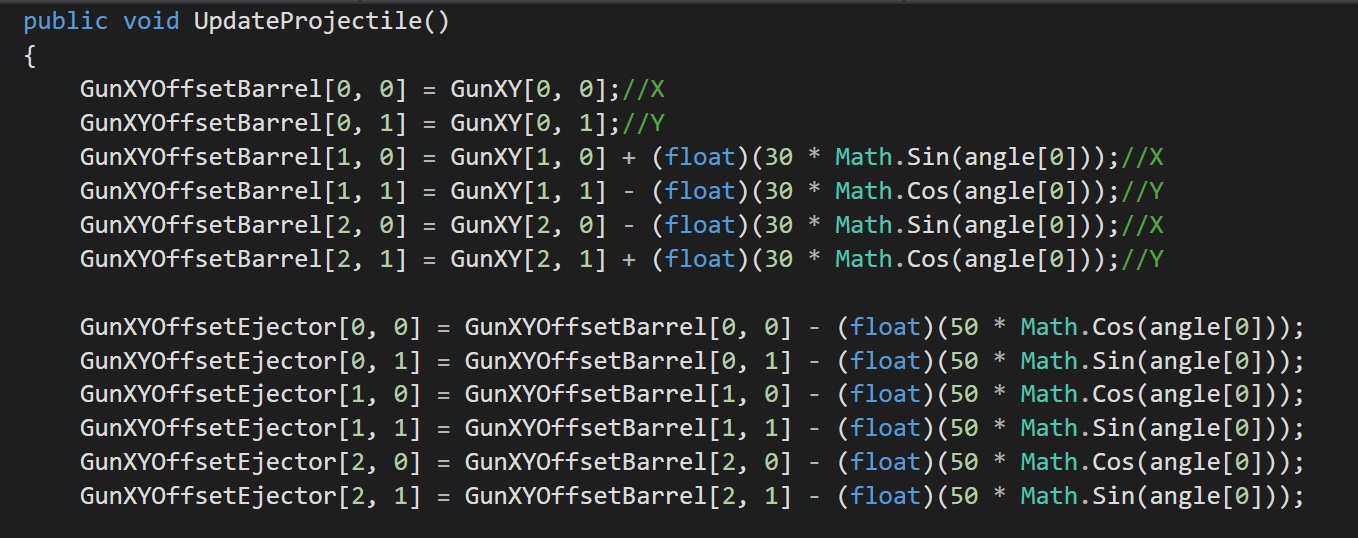
What does this mean? Well it turns out that through the genius of Mathematics if you have an angle in degrees and a length value that would act as a multiplier then (perhaps oddly) passing that angle into Cosine and Sin respectively as X and Y will give you a distance from point A to point B. I thought that was especially nifty as I came up with it myself.
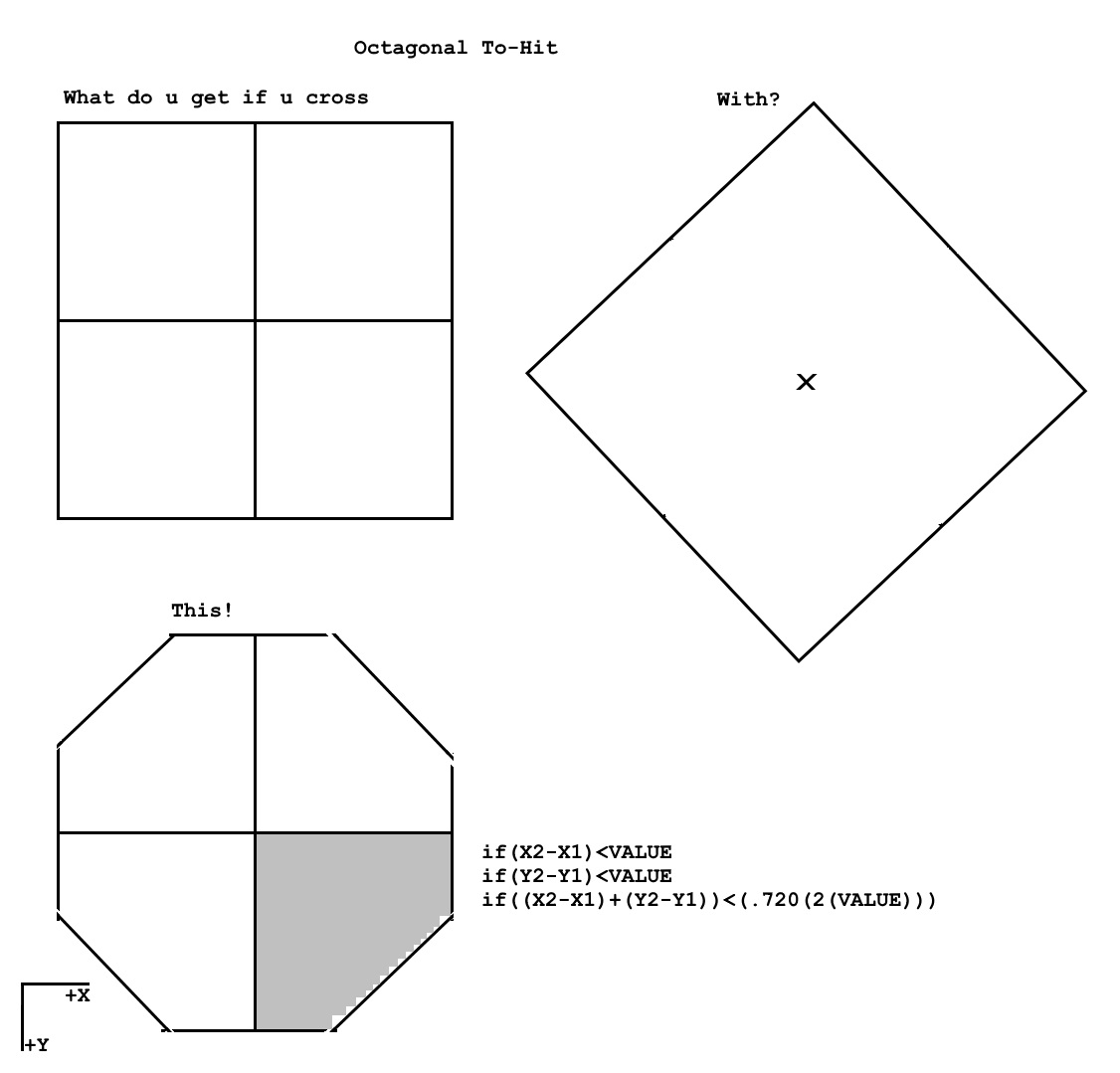
Now what does this mean? Well the biggest bane to the world of Gaming is that too many calculations have to happen in parallel (concurrently) for instance every projectile that comes from the battleship and impacts the ground has to do a check for what is close enough to be impacted with. This particular field of Calculation is known as Collisions.

When referring to the picture above every time a projectile explodes there is no way to avoid doing a calculation to check distance between every single one of those little troopers there to see if the projectile hit the target. The only thing that can be done to mittigate this dilema is to make the calculations performed less processor heavy.
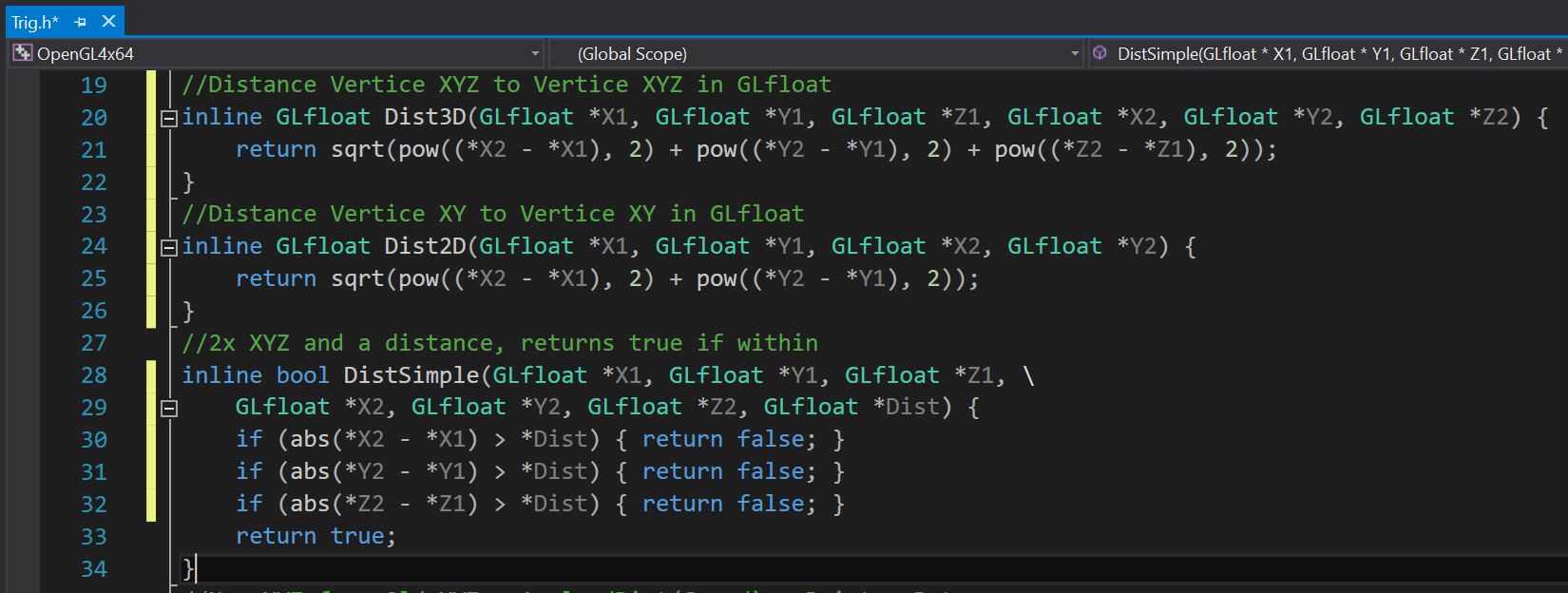
(Note that this is a much more modern snippet of code that i made for VIC & ICTP in the language C++ though the formulas remain the same, GPT is C#)
What you see here are three different (functions) the first one is to get the precise value between two points in XYZ space.
The specific formula is;
Square Root(((X2 - X1)Power 2) + ((Y2 - X1)Power 2) + ((Y2 - X1)Power 2))
A very taxing calculation indeed and gross overkill for a need such as the aformentioned and that was why I came up with The Octagonal To-Hit formula above and also DistSimple() which can be seen directly above which actually checks for a square (or technically Cube) in the name of speed and efficiency.
DistSimple for comparison checks;
if, Absolute Value(X2 - X1) > Distance Specified, terminate calculation
then the same for Y, and in this case also for Z and if it passes all those calculations then a collision has been detected
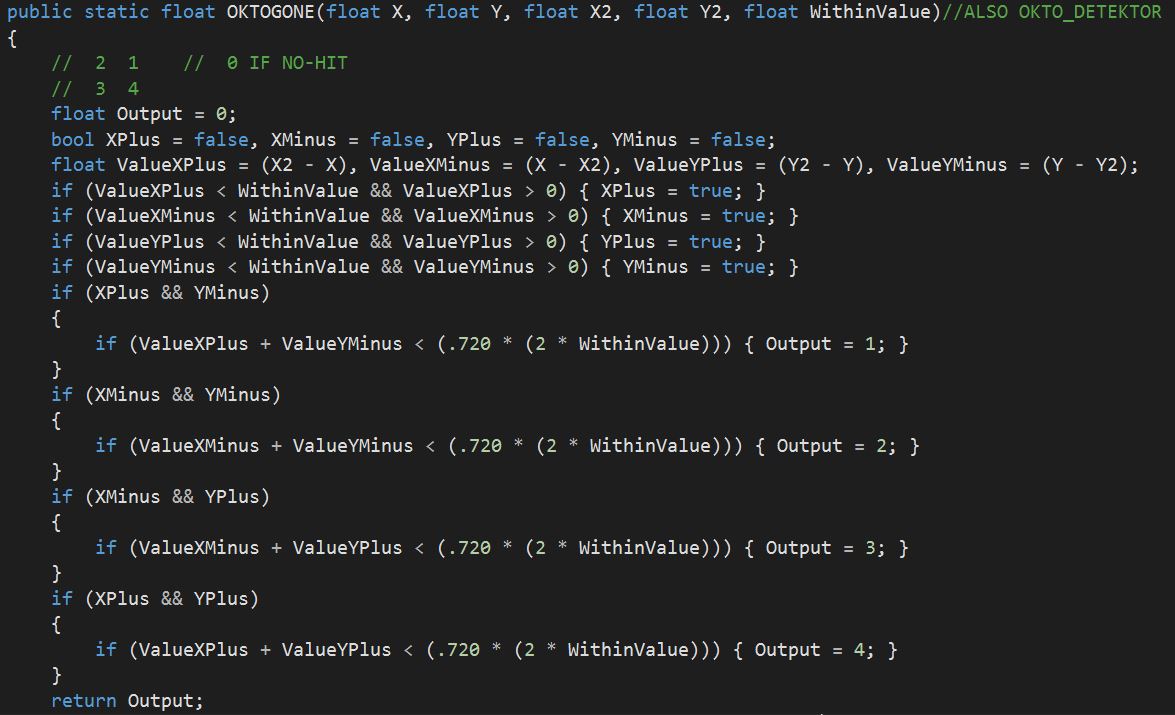
The Octagonal To-Hit formula for comparison is identical in the first two calclations and also that the calculation will terminate upon failing a previous check though then it checks some manner of precise distance in order to see if they are within range diagonally.
For anyone interested below is the implementation of The Octagonal To-Hit formula and do bear in mind that it was one of my earlier pieces of code (also my first experience with C#) though this particular implementation will return which quadrant (or corner) the collision was detected which was important as when the troopers were hit they were propelled in the opposite direction.
Also I have a sneaking suspicion it will impress no mathematicians at all :P
I also made a youtube video of the game itself;
Or the game that preceeded it. Which was the very first game I ever made which was made in the University of Canberra library during the night after my very first GPT Tutorial!